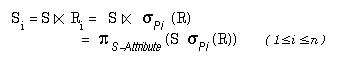5.3 Horizontale Fragmentierung

5.3.2 Abgeleitete horizontale Fragmentierung

Beispiel 5-2

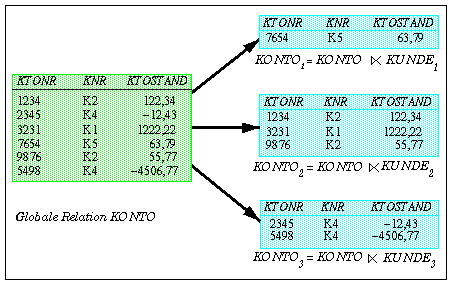
In unserem Bankbeispiel (Abb. 2-1) besteht eine Abhängigkeit zwischen der KONTO- und der KUNDE-Relation über das Kundennummer-Attribut KNR. Dabei ist KNR ein Fremdschlüssel in KONTO, der sich auf den Primärschlüssel von KUNDE bezieht. Eine abgeleitete horizontale Fragmentierung von KONTO orientiert sich daher an der horizontalen Fragmentierung von KUNDE, das heißt, die den Kunden eines Fragmentes zugeordneten Konten werden ebenfalls innerhalb eines Fragmentes zusammengefaßt. Wenn, wie in Beispiel 5-1 der Fall, KUNDE nach Filialen horizontal fragmentiert ist, werden somit alle Konten nach der Filialzugehörigkeit ihrer Kontoinhaber fragmentiert, wie in Abb. 5-3 verdeutlicht. Das Fragment KONTO₂ enthält z.B. alle Konten von Kunden der Filiale "F" (Frankfurt).

Abb. 5-3: Abgeleitete horizontale Fragmentierung der Kontorelation

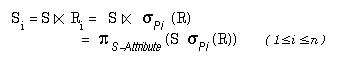
Die zur Definition der Fragmentierung verwendeten Selektionsprädikate P_i beziehen sich hierbei ausschließlich auf Attribute von R, also nicht auf Attribute der zu zerlegenden (abhängigen) Relation S. Die Rekonstruktion der globalen Relation S ergibt sich analog wie für R durch Vereinigung der einzelnen Fragmente S_i. Die Vollständigkeit der Zerlegung ist gewährleistet, falls der Semi-Join zwischen S und R verlustfrei ist, da dann zu jedem S-Tupel ein Verbundpartner in R existiert. Die Verlustfreiheit des Semi-Joins ist gegeben, wenn für den Fremdschlüssel in S keine Nullwerte zulässig sind, da dann aufgrund der referentiellen Integrität ein Verbundpartner in R garantiert ist[18]. In unserem Bankbeispiel ist dies der Fall, da für den Fremdschlüssel KNR in KONTO (Kontoinhaber) sinnvollerweise keine Nullwerte zugelassen werden. Die Disjunktheit der S-Fragmente ergibt sich aus der Disjunktheit der R-Fragmente, da zwischen den beiden Relationen eine N:1-Beziehung besteht.

Ein wesentlicher Vorteil der abgeleiteten horizontalen Fragmentierung liegt darin, daß sie eine effiziente (Equi-)Join-Berechnung zwischen S und R unterstützt. Denn durch die Fragmentierung ist gewährleistet, daß alle zum Fragment R_i gehörenden Tupel der Relation S in Fragment S_i liegen (und umgekehrt). Werden die Fragmente R_i und S_i jeweils dem gleichen Rechner zugeordnet, kann daher eine lokale Join-Berechnung erfolgen. Ferner wird eine lokale Überprüfung der referentiellen Integrität möglich.

Beispiel 5-3

In dem eingeführten Bankbeispiel mit abgeleiteter horizontaler Fragmentierung der KONTO-Relation können Join-Berechnungen zwischen KUNDE und KONTO weitgehend lokal erfolgen, falls die entsprechenden Fragmente jeweils demselben Rechner zugeordnet werden. Dies trifft für die Bestimmung von Kontoangaben zu einem Kunden ebenso zu wie die Ermittlung von Kundenangaben zu einem bestimmten Konto.
Auch die referentielle Integrität kann lokal überwacht werden. Wird ein neues Konto eröffnet (bzw. der Kontoinhaber eines bestehenden Kontos geändert), kann die Gültigkeit der anzugebenden Kundennummer (KNR) lokal geprüft werden. Bei Löschungen in der Kundenrelation (bzw. Änderungen der Kundennummer) können die davon betroffenen Kontosätze lokal ermittelt werden. Somit läßt sich die Zulässigkeit der Operation lokal überprüfen bzw. Folgeänderungen in der Kontorelation können lokal durchgeführt werden.