





6 Verteilte Anfragebearbeitung
6.2 Anfragetransformation
Aufgabe der Anfragetransformation ist die Überführung einer z.B. in SQL deskriptiv formulierten DB-Operation in eine funktional äquivalente Interndarstellung, auf der die weiteren Schritte der Anfragebearbeitung aufbauen. Zur Interndarstellung verwenden wir hier die Relationenalgebra, da sie eine prozedurale Spezifikation der Verarbeitung zuläßt. Insbesondere können die zur Realisierung benötigten relationalen Basisoperatoren (Projektion, Selektion, Join etc.) sowie die Reihenfolge ihrer Bearbeitung spezifiziert werden. Die auf die Anfragetransformation folgende Phase der Daten-Lokalisierung führt im Prinzip ebenfalls eine Anfragetransformation durch, jedoch unter Berücksichtigung der Verteilungsinformation
Abb. 6-2: Teilschritte bei der Anfragetransformation .
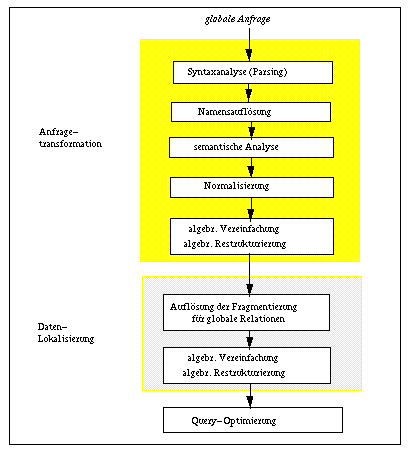
Abb. 6-2 veranschaulicht, daß die Anfragetransformation in mehrere aufeinanderfolgende Teilschritte unterteilt werden kann, wie sie bereits für zentralisierte DBS anfallen [JK84, Hä87]. Dabei werden zunächst die bei der Übersetzung üblichen lexikalischen und syntaktischen Analysen vorgenommen (Parsing), um die syntaktische Korrektheit der Anfrage sicherzustellen. Daran schließt sich die Namensauflösung an, d.h. die Abbildung logischer Objektbezeichnungen in interne Namen. Im verteilten Fall kann dies die Nutzung von Synonymtabellen erfordern, um die global eindeutigen Namen zu generieren (Abb. 4-5). Weiterhin sind - in Abhängigkeit der gewählten Katalogverwaltung - für den Zugriff auf globale Katalogdaten ggf. Kommunikationsvorgänge in Kauf zu nehmen.
Im Rahmen der semantischen Analyse wird geprüft, ob die verwendeten Relationen und Attribute im globalen Schema definiert sind. Falls die Operation auf Sichten (Views) spezifiziert wurde, erfolgt eine Abbildung auf die zugrundeliegenden Basisrelationen. Daneben können bereits einfache Integritätsbedingungen überprüft werden, z.B. die Typverträglichkeit in Vergleichsprädikaten oder die Einhaltung von Wertebereichen. Weiterhin lassen sich zu diesem Zeitpunkt einfache (wertunabhängige) Zugriffskontrollbedingungen überprüfen, soweit sie im globalen Schema festgelegt sind.
Aufgabe der Normalisierung ist es, die Anfrage in ein vereinheitlichtes (normalisiertes, kanonisches, standardisiertes) Format zu überführen, das die Durchführung der nachfolgenden Optimierungsschritte erleichtert. Dies betrifft vor allem die Repräsentation von Selektions- bzw. Join-Bedingungen (WHERE-Klausel in SQL). Hierzu kommen im wesentlichen zwei Alternativen in Betracht: die konjunktive bzw. die disjunktive Normalform. Die konjunktive Normalform ist eine Konjunktion ( - bzw. AND-Verknüpfung) von Disjunktionen (
- bzw. AND-Verknüpfung) von Disjunktionen ( - bzw. OR-Prädikaten):
- bzw. OR-Prädikaten):
(p11  p12
p12  . . .
. . .  p1n)
p1n)  . . .
. . .  (pm1
(pm1  pm2
pm2  . . .
. . .  pmn) ,
pmn) ,
wobei pij einfache Prädikate der Form <Attribut> <Vergleichsoperator> <Attribut bzw. Konstante> darstellen. Die disjunktive Normalform dagegen stellt eine Disjunktion von Konjunktionen dar:
(p11  p12
p12  . . .
. . .  p1n)
p1n)  . . .
. . .  (pm1
(pm1  pm2
pm2  . . .
. . .  pmn).
pmn).
Die beiden Normalformen geben also für Konjunktionen bzw. Disjunktionen unterschiedliche Auswertungsreihenfolgen vor (die jedoch im Zuge der weiteren Optimierung noch geändert werden können). Die Überführung von Bedingungen in eine dieser Normalformen ist einfach möglich durch Anwendung der bekannten Äquivalenzbeziehungen für logische Operationen ( ,
,  ,
, 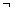 ). Diese sind der Vollständigkeit halber in Abb. 6-3 zusammengestellt.
). Diese sind der Vollständigkeit halber in Abb. 6-3 zusammengestellt.
Abb. 6-3: Äquivalenzbeziehungen für logische Operationen
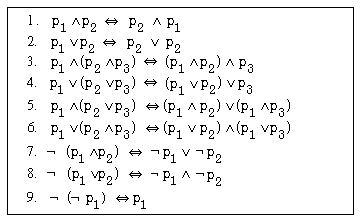
Beispiel 6-1
- In unserer Bankanwendung mit den Relationen KONTO und KUNDE (Kap. 5.3) sollen die Namen der Kontoinhaber aus den Filialen Kaiserslautern und Leipzig ermittelt werden, die ihr Konto überzogen haben. In SQL könnte diese Anfrage folgendermaßen formuliert werden:
- SELECT NAME
FROM KONTO, KUNDE
WHERE KONTO.KNR = KUNDE.KNR AND - KTOSTAND < 0 AND
FILIALE = "KL" OR FILIALE = "L" .
- Die Selektionsbedingung sieht in konjunktiver Normalform folgendermaßen aus:
- KONTO.KNR = KUNDE.KNR
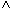 KTOSTAND < 0
KTOSTAND < 0 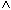 (FILIALE = "KL"
(FILIALE = "KL" 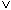 FILIALE = "L").
FILIALE = "L").
- In disjunktiver Normalform dagegen lautet die Bedingung:
- (KONTO.KNR = KUNDE.KNR
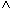 KTOSTAND < 0
KTOSTAND < 0 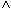 FILIALE = "KL")
FILIALE = "KL") 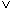
(KONTO.KNR = KUNDE.KNR 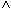 KTOSTAND < 0
KTOSTAND < 0 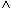 FILIALE = "L").
FILIALE = "L").
Das Beispiel zeigt, daß die Normalisierung zur Wiederholung von Selektions- und Verbundprädikaten führen kann. Für die disjunktive Normalform gilt dies bezüglich mit AND verknüpften Prädikaten (aufgrund von Regel 5 in Abb. 6-3), während die konjunktive Normalform bei OR-Verknüpfungen zur Wiederholung von Teilausdrücken führen kann (Regel 6 in Abb. 6-3). Da in der Praxis AND-Verknüpfungen meist häufiger als OR-Prädikate auftreten, empfiehlt sich die konjunktive Normalform.
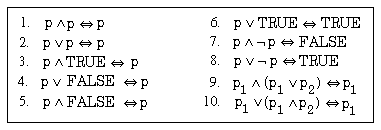
Auf die Normalisierung folgen dann schließlich algebraische Optimierungsschritte, um damit bereits zu effizienter ausführbaren Anfrageformulierungen zu kommen. Als erster Transformationsschritt empfiehlt sich dazu die Durchführung algebraischer Vereinfachungen, um redundante Teilausdrücke zu eliminieren und damit Arbeit bei der Auswertung einzusparen. Eine solche Redundanz kann z.B. durch eine ungeschickte Anfrageformulierung entstanden sein oder durch Anfragen auf Sichten, bei denen die Abbildung auf Basisrelationen zu redundanten Teilausdrücken geführt hat. Die Elimination redundanter Ausdrücke kann über die bekannten und in Abb. 6-4 zusammengestellten Idempotenzregeln erfolgen. Daneben ist es in einfachen Fällen möglich, durch Berücksichtigung von Integritätsbedingungen redundante Ausdrücke zu eliminieren.
Abb. 6-4: Idempotenzregeln für logische Operationen
Beispiel 6-2
- In der Bankanwendung sei die Integritätsbedingung definiert, daß der Kontostand nicht negativ werden darf (was z.B. für Sparbücher sinnvoll ist). Das diese Bedingung definierende Prädikat
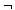 (KTOSTAND < 0)
(KTOSTAND < 0)
kann bei Anfragen, die das Attribut KTOSTAND betreffen, zur Verschärfung der Selektionsbedingung verwendet werden. Dies ist z.B. für die Anfrage aus Beispiel 6-1 möglich, für die sich daraufhin folgende Qualifikationsbedingung in konjunktiver Normalform ergibt:
- KONTO.KNR = KUNDE.KNR
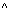
KTOSTAND < 0 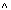
(FILIALE = "KL" 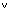 FILIALE = "L")
FILIALE = "L") 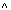
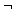 (KTOSTAND < 0).
(KTOSTAND < 0).
- Durch die Anwendung der Regeln 7 und 5 aus Abb. 6-4 kann diese Bedingung sofort zu FALSE ausgewertet werden. Damit kann eine weitere Anfrageverarbeitung eingespart werden, da sich als Ergebnis der Anfrage die leere Menge ergibt.
Ein zweiter Schritt bei der algebraischen Optimierung besteht darin, Restrukturierungen in der Anfragedarstellung vorzunehmen, welche zu einer Verbesserung der Auswertung führen. Diese Restrukturierungen basieren auf heuristischen Optimierungsregeln, die sich als allgemein sinnvoll herausgestellt haben. Zur Anwendung dieser Restrukturierungsregeln sehen wir vor, daß der bis dahin vorliegende Anfrageausdruck in Form eines Operatorbaumes dargestellt wird. In einem solchen Baum, der einen azyklischen Graphen darstellt, bilden die Blattknoten Basisobjekte (Relationen), auf denen die Operatoren angewendet werden. Die Operatoren korrespondieren zu den restlichen (Nicht-Blatt-) Knoten des Baumes. Die gerichteten Kanten spezifizieren ausgehend von den Blättern die Richtung des Datenflusses. Der Wurzelknoten schließlich bestimmt das Gesamtergebnis der Anfrage. Im Rahmen der Fragmentierung hatten wir solche Operatorgraphen bereits kurz kennengelernt (Abb. 5-6).
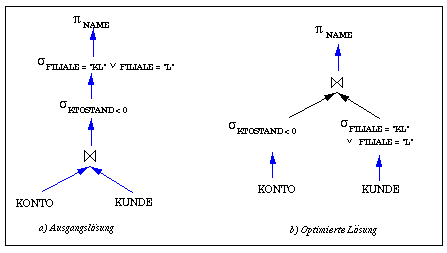
In Abb. 6-5a ist ein möglicher Operatorbaum zur Anfrage aus Beispiel 6-1 gezeigt. Das Beispiel veranschaulicht auch, wie aus einer Anfrage ein Operatorbaum gewonnen werden kann. Zunächst bildet jede der beteiligten Relationen ein Blatt im Operatorbaum (FROM-Klausel in SQL). Der Wurzelknoten entspricht der Projektion auf die auszugebenden Attribute (SELECT-Klausel in SQL). Die Zwischenknoten schließlich korrespondieren zu den Selektions- und Join-Operationen, wie sie in dem normalisierten Qualifikationsausdruck spezifiziert sind (WHERE-Klausel von SQL).
Abb. 6-5: Beispiel von Operatorbäumen
Zu einer bestimmten Anfrage existiert in der Regel eine große Anzahl funktional äquivalenter Operatorbäume. Dies ergibt sich aufgrund von Äquivalenzbedingungen für relationale Operatoren, wie sie in einer Auswahl in Abb. 6-6 zusammengestellt sind. Die Optimierung einer Anfrage erfolgt immer unter Berücksichtigung dieser Regeln, um die funktionale Äquivalenz bei der Durchführung von Anfragetransformationen zu gewährleisten. Ein naiver Ansatz zur Query-Optimierung wäre die Bestimmung und Bewertung sämtlicher äquivalenter Opertorbäume, um darunter den günstigsten auszuwählen. Dieser Ansatz scheidet jedoch aufgrund des unverhältnismäßig hohen Aufwandes aus. Durch Anwendung von Heuristiken kann man jedoch bereits vielfach eine Vorauswahl treffen, so daß sich das Optimierungsproblem vereinfacht.
Abb. 6-6: Äquivalenzbeziehungen für relationale Operatoren (Auswahl)

Solche Heuristiken zur Restrukturierung von Operatorbäumen können bereits im Rahmen der algebraischen Optimierung vorgenommen werden, bei der physische Aspekte wie Datenverteilung oder Indexstrukturen unberücksichtigt bleiben. Hierzu haben sich u.a. folgende Ansätze als effektiv erwiesen:
- Möglichst frühzeitige Ausführung von Selektionsoperationen, um eine Reduzierung des weiterzuverarbeitenden Datenvolumens zu erreichen (Anwendung der Regeln 5, 8 und 10 in Abb. 6-6).
- Frühzeitige Durchführung von Projektionen zur Reduzierung des Datenvolumens, sofern die (teuere) Eliminierung von Duplikaten nicht erforderlich ist (Regeln 9 und 11 in Abb. 6-6). Dabei sollten Projektionen jedoch nicht vor Selektionen vorgenommen werden.
- Zusammenfassung mehrerer Selektionen und Projektionen auf demselben Objekt (Regeln 2 und 4 in Abb. 6-6).
- Bestimmung gemeinsamer Teilausdrücke, wie sie etwa durch die Normalisierung eingeführt wurden, um diese nur einmal zu berechnen.
Die frühzeitige Reduzierung der Datenmengen durch Vorziehen einstelliger Operatoren wie Selektion und Projektion ist im verteilten Fall i.a. noch effektiver als schon in zentralisierten DBS, weil damit auch der Kommunikationsumfang vermindert werden kann. Der in Abb. 6-5a gezeigte Operatorbaum läßt sich durch Anwendung der genannten Heuristiken und unter Beachtung der Äquivalenzbedingungen leicht verbessern. Durch Vorziehen der Selektionsbedingungen ergibt sich so die in Abb. 6-5b dargestellte Lösung. Eine weitere Optimierung wäre durch teilweises Vorziehen von Projektionen möglich (Regel 11).














 - bzw. AND-Verknüpfung) von Disjunktionen (
- bzw. AND-Verknüpfung) von Disjunktionen ( - bzw. OR-Prädikaten):
- bzw. OR-Prädikaten):  p12
p12  . . .
. . .  p1n)
p1n)  . . .
. . .  (pm1
(pm1  pm2
pm2  . . .
. . .  pmn) ,
pmn) , p12
p12  . . .
. . .  p1n)
p1n)  . . .
. . .  (pm1
(pm1  pm2
pm2  . . .
. . .  pmn).
pmn). ,
,  ,
, 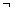 ). Diese sind der Vollständigkeit halber in Abb. 6-3 zusammengestellt.
). Diese sind der Vollständigkeit halber in Abb. 6-3 zusammengestellt.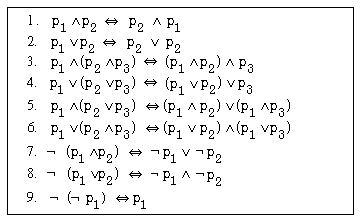
 KTOSTAND < 0
KTOSTAND < 0  (FILIALE = "KL"
(FILIALE = "KL"  FILIALE = "L").
FILIALE = "L").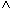 KTOSTAND < 0
KTOSTAND < 0 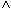 FILIALE = "KL")
FILIALE = "KL") 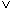
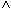 KTOSTAND < 0
KTOSTAND < 0 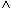 FILIALE = "L").
FILIALE = "L").
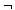 (KTOSTAND < 0)
(KTOSTAND < 0) 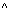
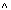
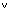 FILIALE = "L")
FILIALE = "L") 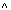
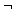 (KTOSTAND < 0).
(KTOSTAND < 0). 






