





18.2 Parallelisierung unärer relationaler Operatoren
18.2.3 Aggregatfunktionen
Die Berechnung von Aggregat- bzw. Built-In-Funktionen (MIN, MAX, SUM, COUNT, AVG) ist bei horizontaler Partitionierung ebenfalls leicht parallelisierbar. Dazu nehmen wir an, daß Q (R) ein Attribut der Relation R sei, auf dem die Built-In-Funktion anzuwenden sei. Die parallele Berechnung von Extremwerten (MIN, MAX) ist dann stets problemlos möglich, da gilt:
- MIN (Q(R)) = MIN (MIN (Q(R1), ... , MIN (Q(Rn) )
und
- MAX (Q(R)) = MAX (MAX (Q(R1), ... , MAX (Q(Rn) ).
Das bedeutet, daß auf jeder Partition Ri parallel das lokale Minimum bzw. Maximum berechnet werden kann. Abschließend wird dann aus diesen lokalen Ergebnissen das globale Minimum bzw. Maximum bestimmt. Die parallele Berechnung von SUM, COUNT und AVG ist in analoger Weise möglich, wenn keine Duplikateliminierung erforderlich ist:
- SUM (Q(R)) =
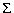 SUM (Q(Ri))
SUM (Q(Ri))
- COUNT (Q(R)) =
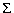 COUNT (Q(Ri))
COUNT (Q(Ri))
- AVG (Q(R)) = SUM (Q(R)) / COUNT (Q(R))
Anderenfalls ist, wie bei der Projektion diskutiert, zuerst die Entfernung von Duplikaten vorzunehmen.






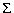 SUM (Q(Ri))
SUM (Q(Ri))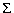 COUNT (Q(Ri))
COUNT (Q(Ri))





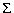 SUM (Q(Ri))
SUM (Q(Ri))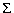 COUNT (Q(Ri))
COUNT (Q(Ri))




