





18.3 Parallele Joins
18.3.2 Join-Berechnung mit dynamischer Partitionierung
Im häufigen Fall des Equi-Joins (Gleichverbund) wird eine parallele Join-Berechnung ohne Replikation einer Relation möglich. Stattdessen genügt eine partitionierte Umverteilung der Eingabedaten, so daß jedes Tupel nur an einen anstatt an n Join-Rechner verschickt wird. Allerdings sind dabei im allgemeinen Fall beide Relationen umzuverteilen, während die Replikation auf die kleinere Relation beschränkt war. Ein Vorteil liegt darin, daß die Anzahl der Join-Prozessoren im allgemeinen Fall frei wählbar ist. Wir beschreiben den Ansatz im folgenden für Shared-Nothing; eine Übertragung auf Shared-Everything und Shared-Disk ist ähnlich möglich wie oben diskutiert. Zunächst betrachten wir den allgemeinen Ansatz mit einer Umverteilung beider Eingaberelationen. Danach werden Spezialfälle diskutiert, wenn für eine oder beide Relationen das Join-Attribut als Verteilattribut vorliegt.
Abb. 18-3: Parallele Join-Berechnung mit dynamischer Partitionierung der Eingaberelationen
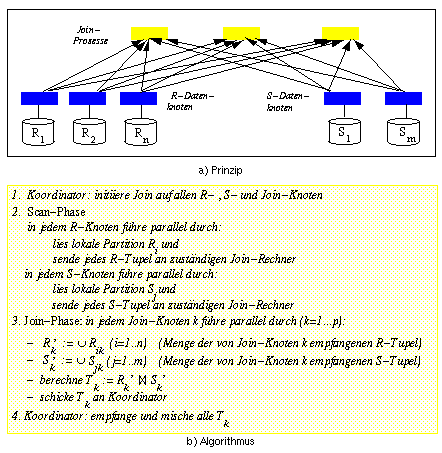
Wir gehen wiederum von einem Join zwischen R und S mit n bzw. m Partitionen aus. Die Join-Berechnung soll nun parallel auf p Prozessoren stattfinden. Dazu lesen die Datenknoten von R und S zunächst in der Scan-Phase ihre Partitionen parallel ein und verteilen die R- bzw. S-Tupel gemäß derselben Verteilungsfunktion f auf dem Join-Attribut unter den p Join-Prozessoren (Abb. 18-3a). Die Verteilungsfunktion bildet jeden Wert des Join-Attributs auf eine Zahl zwischen 1 und p ab, die den zuständigen Join-Prozessor kennzeichnet. Damit ist gewährleistet, daß R- und S-Tupel mit übereinstimmendem Join-Attributwert demselben Join-Prozessor zugeordnet werden. Der eigentliche Verbund kann somit an den Join-Prozessoren wieder parallel mit einem beliebigen lokalen Verfahren durchgeführt werden (Join-Phase). Das Gesamtergebnis der Join-Operation erhält man erneut durch Mischen der Teilergebnisse aller Join-Prozesse.
Die genannten Schritte sind im Algorithmus in Abb. 18-3b noch einmal dargestellt. In Schritt 3 wurden die an Join-Knoten k aufgrund der Umverteilung entstehenden temporären Partitionen mit Rk' und Sk' (k=1 ... p) bezeichnet, da sie sich anders als die an den Datenknoten vorliegenden Partitionen Ri bzw. Sj (i=1..n; j=1..m) zusammensetzen. Beim Einsatz von Pipeline-Parallelität ist es nicht notwendig, daß die in Schritt 3 gezeigten Vereinigungsoperatoren vor der Join-Berechnung vollständig ausgeführt sind (d.h., alle Eingabetupel vorliegen). Dies wäre jedoch erforderlich, wenn ein Sort-Merge-Ansatz zur lokalen Join-Berechnung verwendet werden soll, da hierfür die Eingaberelationen zunächst sortiert werden müssen[83].
Als Verteilungsfunktion zur dynamischen Datenumverteilung kommt eine Hash-oder eine Bereichspartitionierung in Betracht. Die Hash-basierte Verteilung läßt sich über eine Hash-Funktion einfach realisieren und wird in einigen existierenden Systemen verwendet (Teradata, Tandem). Jedoch kann es damit leicht zu Skew-Effekten kommen, wenn eine "schiefe" Werteverteilung für das Join-Attribut vorliegt. Bei bekannter Werteverteilung kann dieser Nachteil durch eine Bereichspartitionierung eher verhindert werden, indem die Wertebereichsintervalle so gewählt werden, daß jeweils etwa gleich viel Tupel pro Partition entfallen. Diese Bestimmung einer solchen Partitionierung ist dafür wieder entsprechend aufwendig [DNSS92].
Der Ansatz der dynamischen Partitionierung weist ein hohes Potential zur Lastbalancierung auf. Denn sowohl die Anzahl der Join-Prozessoren p als auch die Auswahl der Join-Rechner selbst sind dynamisch wählbare Parameter, die in Abhängigkeit des Systemzustandes festgelegt werden können. So wurde in [RM93] festgestellt, daß es sich im Mehrbenutzerbetrieb zur Reduzierung des Kommunikationsaufwandes empfiehlt, die Anzahl der Join-Knoten umso geringer zu wählen, je höher die Prozessoren ausgelastet sind. Hierzu wurde eine Heuristik angegeben, die als Default-Wert für p den optimalen Parallelitätsgrad des Einbenutzerbetriebes verwendet. Dieser wird dynamisch proportional zur mittleren CPU-Auslastung reduziert, v.a. im Auslastungsbereich von über 50%. Zur Join-Verarbeitung selbst wurden daneben die p am geringsten ausgelasteten Rechner verwendet.
Spezialfälle
Der Nachteil des allgemeinen Ansatzes liegt darin, daß beide Eingaberelationen vollständig umverteilt werden müssen, was für große Relationen einen sehr hohen Kommunikationsaufwand verursachen kann. Eine deutliche Reduzierung des Kommunikationsumfangs ist jedoch möglich, wenn für eine der beiden Relationen, z.B. R, die Verteilung auf dem Join-Attribut definiert wurde, d.h. das Verteilungs- mit dem Join-Attribut übereinstimmt. In diesem Fall ist nur eine Umverteilung der zweiten Relation S notwendig, wenn die Join-Verarbeitung auf den R-Knoten erfolgt. Die Funktion zur dynamischen Umverteilung von S muß dabei mit der Fragmentierungs- und Allokationsstrategie für R übereinstimmen (Hash- oder Bereichspartitionierung), um sicherzustellen, daß zusammengehörige Tupel auch an dem selben R-Rechner verarbeitet werden. Allerdings geht die Reduzierung des Kommunikationsaufwandes einher mit dem Verlust dynamischer Lastbalancierungsmöglichkeiten, da die Join-Rechner nicht mehr frei wählbar sind.
Der Kommunikationsaufwand zur Datenumverteilung wird vollständig umgangen, wenn die Verteilungsattribute beider Relationen mit dem Join-Attribut übereinstimmen und eine übereinstimmende Fragmentierung und Allokation verwendet wird. Dabei müssen die zusammengehörigen Tupel beider Relationen jeweils demselben Datenknoten zugeordnet sein. Dies wird durch eine abgeleitete horizontale Fragmentierung unterstützt (Kap. 5.3).
[83] Da beim Sort-Merge-Join eine Sortierung der Eingaberelationen auf dem Join-Attribut vorliegt, kann ein Equi-Join durch einmaliges Lesen beider Relationen berechnet werden. Das Lesen erfolgt schritthaltend in beiden Relationen, wobei zu einem Join-Attribut-Wert der ersten Relation jeweils die zugehörigen Treffer in der zweiten Eingabe ermittelt werden [ME92].



















