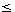 SF
SF 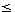 1) zu ermitteln, der angibt, welcher Anteil der Relation sich für eine bestimmte Bedingung qualifiziert[23]. Sei Card (R) die Kardinalität von Relation R und SF (p) der Selektivitätsfaktor für Prädikat p (auf R) dann gilt:
1) zu ermitteln, der angibt, welcher Anteil der Relation sich für eine bestimmte Bedingung qualifiziert[23]. Sei Card (R) die Kardinalität von Relation R und SF (p) der Selektivitätsfaktor für Prädikat p (auf R) dann gilt: 





6 Verteilte Anfragebearbeitung
Ein Problem bei der Query-Optimierung im verteilten Fall ergibt sich durch die Trennung zwischen globaler und lokaler Optimierung, wie sie für eine möglichst hohe Knotenautonomie erforderlich ist. Denn damit kann der globale Optimierer die Kosten eines Ausführungsplanes nur partiell abschätzen, im wesentlichen nämlich die Kommunikationskosten. Dies kann dazu führen, daß ein bezüglich der globalen Kosten optimaler Plan hohe lokale Kosten verursacht, während alternative Strategien trotz höherer Kommunikationskosten insgesamt billiger abschneiden. Da der globale Optimierer i.a. keine Kenntnisse über lokale Schemaangaben der einzelnen Rechner hat, kann über die Nutzung von Indexstrukturen oder die Auswahl einer lokalen Join-Strategie (z.B. Nested-Loop-, Sort-Merge- oder Hash-Join) nur der lokale Optimierer entscheiden. Der globale Optimierer bestimmt dagegen vor allem die Ausführungsreihenfolge sowie die Ausführungsorte der einzelnen Operatoren sowie die Methode des Datenaustauschs. Bei einfachen Operatoren wie Selektion und Projektion ist dabei der Ausführungsort durch die Datenalllokation gegeben. Hier bestehen nur im Falle von Replikation Auswahlmöglichkeiten. Für komplexere Berechnungen wie Join-Bildung besteht dagegen ein größeres Optimierungspotential, wie in Kap. 6.5 gezeigt wird.
Zur Bewertung alternativer Ausführungspläne ist ein geeignetes Kostenmodell erforderlich. Im Prototyp R* wurde hierzu die gewichtete Summe aus CPU-, E/A- und Kommunikationskosten verwendet [ML86]:
Dabei sind die Kommunikationskosten über zwei Komponenten berücksichtigt, die Anzahl der Nachrichten sowie den Nachrichtenumfang. Die einzelnen Gewichte Wx, die z.B. Zeiteinheiten darstellen können, sind auf die jeweilige Umgebung abzustimmen (Leistungsfähigkeit der CPUs, des Kommunikationsnetzwerkes etc). Bei Trennung von globaler und lokaler Optimierung können, wie erwähnt, bei der globalen Optimierung lediglich die Kommunikationskosten abgeschätzt werden. In geographisch verteilten Systemen ist dies i.a. keine signifikante Einschränkung, da hier die teuere Kommunikation oft einen Großteil der Verarbeitungsdauer verursacht. In lokal verteilten Systemen gilt dies sicherlich nicht mehr, so daß CPU- und E/A-Kosten auch für globale Optimierungsentscheidungen zu berücksichtigen sind. In diesem Fall spielt die Knotenautonomie jedoch auch eine untergeordnete Rolle, so daß ggf. auf die Trennung zwischen globaler und lokaler Optimierung verzichtet werden kann[22].
Wenn die Gewichte Wx in Zeiteinheiten angegeben werden, dann stellt obige Kostenformel eine grobe Abschätzung hinsichtlich der sequentiellen Bearbeitungszeit dar (ohne Wartesituationen aufgrund konkurrierender Operationen). Allerdings kann bei Parallelisierung einzelner Teilschritte diese Bearbeitungszeit möglicherweise signifikant reduziert werden. Um dies bei der Kostenbewertung zu berücksichtigen, müßten für parallelisierte Teilschritte die Kosten gegenüber einer sequentiellen Bearbeitung entsprechend geringer angesetzt werden.
Die Kosten relationaler Operatoren sind wesentlich vom Umfang der zu verarbeitenden Datenmenge bestimmt. Um eine Kostenbewertung vornehmen zu können, müssen daher entsprechende Statistiken vorliegen, insbesondere hinsichtlich der Kardinalität (Tupelanzahl) der einzelnen Relationen und Fragmente, der Größe einzelner Attribute und Tupel sowie bezüglich der Häufigkeitsverteilung von Attributwerten. Aus diesen Angaben werden bei der Optimierung dann für die einzelnen Ausführungspläne die Größe von Zwischenergebnissen ermittelt, um wiederum die Kosten für nachfolgend auszuführende Operationen abzuschätzen.
Der Bestimmung von Zwischenergebnis-Größen kommt somit eine wesentliche Bedeutung zu. Bei Selektionen ist dabei ein sogenannter Selektivitätsfaktor SF (0 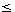 SF
SF 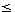 1) zu ermitteln, der angibt, welcher Anteil der Relation sich für eine bestimmte Bedingung qualifiziert[23]. Sei Card (R) die Kardinalität von Relation R und SF (p) der Selektivitätsfaktor für Prädikat p (auf R) dann gilt:
1) zu ermitteln, der angibt, welcher Anteil der Relation sich für eine bestimmte Bedingung qualifiziert[23]. Sei Card (R) die Kardinalität von Relation R und SF (p) der Selektivitätsfaktor für Prädikat p (auf R) dann gilt:
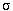 p (R)) = SF (p) * Card (R).
p (R)) = SF (p) * Card (R).
Da es nicht möglich ist, für jedes beliebige Prädikat Selektivitätsstatistiken zu führen, ist man auf Abschätzungen angewiesen. Hierzu benötigt man für jedes Attribut A wenigstens die Anzahl unterschiedlicher Attributwerte (= Card ( A (R)) sowie den minimalen und maximalen Attributwert. Unter der Annahme, daß die einzelnen Attributwerte gleichverteilt vorkommen, kann man dann z.B. die Selektivität von exakten Anfragen (exact match queries) bzw. Bereichsanfragen bezüglich einer Eingabekonstanten k folgendermaßen abschätzen (k liege im Intervall zwischen Min (A) und Max (A)):
A (R)) sowie den minimalen und maximalen Attributwert. Unter der Annahme, daß die einzelnen Attributwerte gleichverteilt vorkommen, kann man dann z.B. die Selektivität von exakten Anfragen (exact match queries) bzw. Bereichsanfragen bezüglich einer Eingabekonstanten k folgendermaßen abschätzen (k liege im Intervall zwischen Min (A) und Max (A)):
 A (R))
A (R))
 p(B)) = SF (p(A)) * SF (p(B)).
p(B)) = SF (p(A)) * SF (p(B)).Ähnliche Abschätzungen können auch für die anderen relationalen Operatoren vorgenommen werden. Für den Join zwischen zwei Relationen ist ein sogenannter Join-Selektivitätsfaktor JSF zu ermitteln, der angibt, welcher Anteil aus dem kartesischen Produkt der Relationen im Join-Ergebnis enthalten ist:
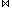 S) = JSF * Card (R) * Card (S).
S) = JSF * Card (R) * Card (S).
Einen wichtigen Spezialfall hierbei bilden N:1-Joins (hierarchische Joins) aufgrund einer Fremdschlüssel/Primärschlüsselbeziehung, bei denen zu jedem Wert des Join-Attributs der größeren Relation genau ein Verbundpartner in der kleineren Relation existiert. In diesem Fall gilt:
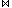 S) = Max (Card (R), Card (S)).
S) = Max (Card (R), Card (S)).Problematisch bei der skizzierten Vorgehensweise ist, daß die erwähnten Annahmen (Gleichverteilung von Attributwerten, Unabhängigkeit verschiedener Attribute) oft nicht gegeben sind. Folglich können die darauf basierenden Schätzungen starken Fehlern unterworfen sein, so daß es ggf. zur Auswahl ungünstiger Pläne kommt. Diese Problematik stellt sich bereits in zentralisierten DBS; eine Verbesserung der Situation kann z.B. unter Verwendung genauerer Statistiken über die Werteverteilungen erfolgen [LNS90]. Weiterhin könnten Statistiken zur Join-Selektivität mit vertretbarem Aufwand geführt werden, da die Anzahl unterschiedlicher (nicht-hierarchischer) Join-Verknüpfungen oft begrenzt ist.





