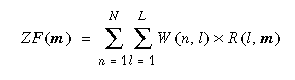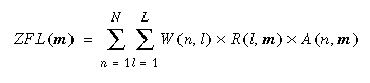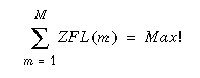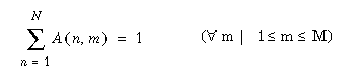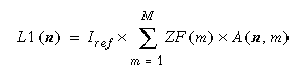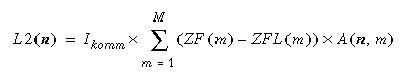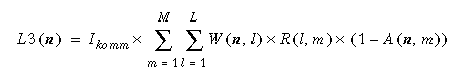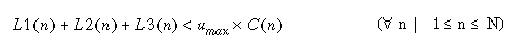5.7 Bestimmung der Datenverteilung
5.7.2 Festlegung der Allokation
Die Bestimmung einer Datenallokation in verteilten Systemen ist ein intensiv untersuchtes Optimierungsproblem [DF82, Wa84, Ap88, HR88]. Das Allokationsproblem wurde meist für die Zuordnung ganzer Dateien betrachtet (file allocation problem, FAP); die entwickelten Ansätze lassen sich oft jedoch auch zur Allokation von Fragmenten heranziehen. Das Optimierungsziel ist i.a. die Minimierung einer globalen Kostenfunktion unter Berücksichtigung bestimmter Randbedingungen. Bei der Ausgestaltung von Kostenfunktion sowie den betrachteten Randbedingungen bestehen erhebliche Unterschiede zwischen den einzelnen Ansätzen. Im einfachsten Fall wird lediglich eine Minimierung von Kommunikationsvorgängen durch Unterstützung von Lokalität angestrebt; komplexere Modelle berücksichtigen daneben auch die Speicherkosten sowie lokale Verarbeitungskosten. Mögliche Randbedingungen sind die Beachtung knotenspezifischer Obergrenzen hinsichtlich der Speicher- oder Verarbeitungskapazität, um z.B. eine Lastbalancierung zu unterstützen.
Um die prinzipielle Vorgehensweise zu veranschaulichen, soll im folgenden ein einfacher Ansatz zur Datenallokation skizziert werden. Wir beschränken uns dabei auf die partitionierte Allokation von Fragmenten (keine Replikation)[19]. Als Eingabe werden folgende Größen benötigt:
- Anzahl der Transaktionstypen L, Anzahl der Knoten N, Anzahl der Fragmente M
- Lastverteilung W (N*L Einträge). Eintrag W (n, l) gibt an, mit welcher Häufigkeit Transaktionstyp l an Knoten n gestartet wird
- Referenzmatrix R (L*M Einträge): Zugriffsverteilung zwischen Transaktionstypen und Fragmenten. Eintrag R (l, m) gibt an, wieviele Zugriffe pro Ausführung von Transaktionstyp l im Mittel auf Fragment m entfallen
- Mittlere Anzahl von Instruktionen für eine lokale DB-Referenz: Iref
- Mittlere Anzahl von Instruktionen zur Kommunikation, die pro externem Zugriff im beauftragenden sowie im ausführenden Rechner anfallen: Ikomm
- CPU-Kapazität von Knoten n: C (n) (1
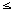 n
n 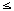 N)
N)
- maximale CPU-Auslastung pro Knoten: umax (0 < umax < 1).
Als Ausgabe soll eine Allokation von Fragmenten zu Rechnern bestimmt werden:
- Allokationsmatrix A (N*M Einträge). Eintrag A (n, m) = 1 (0), falls Fragment m an Knoten n (nicht) gespeichert werden soll.
Als Optimierungsziel streben wir dabei die Minimierung des Kommunikationsaufwandes an, d.h. die Maximierung lokaler Fragmentzugriffe. Auf Fragment m besteht insgesamt folgende Zugriffsfrequenz:
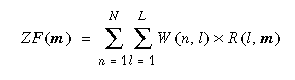
Davon sind jedoch nur die Zugriffe in dem Knoten n lokal, dem Fragment m zugewiesen wurde, das heißt, für den A (n,m) = 1 gilt. Damit ergibt sich folgende Häufigkeit lokaler Zugriffe auf Fragment m:
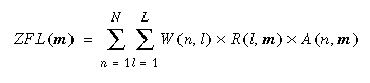
Das Optimierungsziel, die Summe lokaler Fragmentzugriffe zu maximieren, lautet demnach:
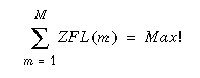
Dabei sind zwei Nebenbedingungen einzuhalten. Zum einen muß jedes Fragment genau einem Knoten zugeordnet werden (partitionierte Allokation):
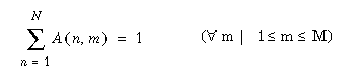
Daneben muß eine Lastbalancierung erreicht werden, das heißt, kein Rechner darf überlastet werden. Die Auslastung eines Rechners setzt sich in unserem Modell aus drei Komponenten, L1, L2 und L3, zusammen. Der erste Lastanteil L1 entsteht durch die eigentlichen Fragmentzugriffe, die aufgrund der Datenallokation an Rechner n auszuführen sind:
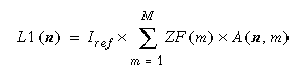
Lastanteil L2 entsteht durch den Kommunikationsaufwand für Zugriffe auf lokale Datenfragmente durch externe Transaktionen:
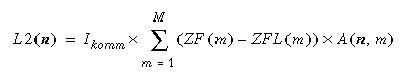
Der dritte Anteil L3 schließlich entsteht für Kommunikationsvorgänge lokaler Transaktionen, um auf extern allokierte Fragmente zuzugreifen:
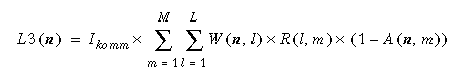
Die zweite Nebenbedingung lautet somit insgesamt
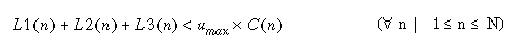
Die exakte Lösung dieses ganzzahligen Optimierungsproblems ist sehr aufwendig, so daß sich die Anwendung einfacherer Heuristiken empfiehlt, welche zu geringen Berechnungskosten eine gute Lösung liefern. Wir skizzieren dazu im folgenden eine einfache Strategie. Wir benötigen dazu Hilfsvariablen CUn, die für jeden Rechner die CPU-Belastung festhalten, die sich aufgrund der bereits vorgenommenen Allokationen ergibt. Der Algorithmus läuft in folgenden Schritten ab:
1. Berechne aus der Lastverteilung L und der Referenzverteilung R zunächst für jedes Fragment m die Zugriffshäufigkeit ZF (m).
2. Bestimme das nächste, noch nicht allokierte Fragment m mit der höchsten Zugriffsfrequenz ZF (m).
3. Berechne für jeden Rechner die lokale Zugriffsfrequenz ZFL (m), die sich durch Allokation von Fragment m an diesen Rechner ergibt, ebenso die sich daraus ergebende Erhöhung der CPU-Auslastung.
4. Ordne das Fragment demjenigen Rechner zu, für den sich der größte Anteil lokaler Zugriffe ergibt, ohne daß sich ein Überschreiten der maximalen CPU-Auslastung ergibt. Ergänze die Allokationsmatrix A und die CU-Werte für die getroffene Allokation.
5. Falls noch weitere Fragmente zuzuordnen sind, gehe zu Schritt 2. Ansonsten ist die Berechnung der Allokation beendet.
Beispiel 5-8
- Der vorgestellte Allokationsansatz soll auf die in Abb. 5-7 gezeigte Last- und Referenzverteilung angewendet werden (L=4, N=3, M=5). Wir nehmen ferner an, daß Iref = 10000, Ikomm = 2500, C(n)=30 MIPS und umax = 0.8 gilt (jeder Rechner soll also höchstens zu 80% ausgelastet werden). In Schritt 1 berechnen wir zunächst die Zugriffshäufigkeiten auf die Fragmente, wobei sich das in Abb. 5-7c gezeigte Resultat ergibt. Da die Fragmente in der Reihenfolge ihrer Zugriffshäufigkeit allokiert werden, ist zunächst Fragment F4 zuzuordnen. Von den 1400 Zugriffen pro Sekunde auf diesem Fragment können 210 in Rechner R1, 400 in R2 und 790 in R3 lokal bearbeitet werden, wenn F4 dem jeweiligen Knoten zugeordnet wird. Somit wird F4 Rechner R3 zugewiesen, wodurch sich dort bereits eine Last von CU3=15,525 MIPS ergibt (14 MIPS für die Fragmentzugriffe, der Rest für Kommunikation aufgrund von externen F4-Zugriffen). Kommunikationsbelastungen für Zugriffe auf F4 fallen auch in R1 und R3 an: CU1=0,525 MIPS, CU2=1,0 MIPS.
- Bei der Zuweisung von Fragment F1 ergibt sich für R2 der höchste Anteil lokaler Zugriffe. Nach dieser Allokation besteht folgende Lastsituation: CU1=1,5875 MIPS; CU2=14,0 MIPS; CU3=16,0625 MIPS. Fragment F5 geht danach an R1 (550 von 1010 Zugriffen lokal), woraus folgende Auslastungswerte resultieren: CU1=12,8375 MIPS; CU2=14,75 MIPS; CU3=16,4625 MIPS.
- Für die Allokation von F3 ergäbe sich anschließend für Rechner R2 der höchste Anteil lokaler Verarbeitung, jedoch würde sich durch diese Allokation die Auslastung um 10,7 MIPS in R2 erhöhen, so daß der Auslastungsgrenzwert von 24 MIPS überschritten wäre. Die Zuordnung zum nächstbesseren Kandidaten R1 kann dagegen durchgeführt werden. Danach gilt CU1=23,7125 MIPS; CU2=15,8 MIPS; CU3=16,8875 MIPS. Abschließend erfolgt noch die Allokation von F2 zu Rechner R2, wodurch sich insgesamt folgende projezierte Rechnerauslastung ergibt: CU1=23,7125 MIPS (79 %); CU2=20,45 MIPS (68 %); CU3=17,3375 MIPS (58%).
- Die Allokation ordnet also R1 die Fragmente F3 und F5, R2 die Fragmente F1 und F2 sowie R3 Fragment F4 zu. Der Anteil lokaler Zugriffe ist für die Beispiellast relativ gering (49,45%), so daß ein hoher Kommunikations-Overhead entsteht (12,4 MIPS der insgesamt 61,5 MIPS).
Abb. 5-7: Beispiel einer Last- und Referenzverteilung

Im Beispiel wurden die Kommunikationskosten pro Zugriff (Ikomm) relativ gering angesetzt, da i.a. nicht jede externe Referenz einen eigenen Kommunikationsvorgang verursacht, sondern i.a. mehrere Fragmentzugriffe pro (externer) Teiloperation durchgeführt werden. Die zur Lastbalancierung eingeführte Nebenbedingung sieht nicht vor, daß alle Rechner möglichst gleichmäßig ausgelastet werden, sondern daß die Auslastung pro Rechner einen bestimmten Grenzwert nicht überschreitet. Dieser weniger restriktive Ansatz gestattet generell einen höheren Anteil an lokalen Zugriffen.
Es ist möglich, daß der Algorithmus nicht erfolgreich zu Ende kommt, wenn nämlich in Schritt 4 für keinen der Rechner eine Zuordnung möglich ist, ohne daß seine Auslastungsgrenze überschritten wird. Dies deutet daraufhin, daß die vorgesehene CPU-Kapazität der Rechner für die unterstellte Last nicht ausreicht. Möglicherweise kann auch durch eine Verfeinerung der Fragmentierung und damit der zuzuordnenden Lastanteilen eine Lösung gefunden werden. Ein solcher Schritt kann auch sinnvoll sein, um den Anteil lokaler Zugriffe zu erhöhen. Voraussetzung für die erneute Anwendung des Allokationsalgorithmus' ist dann natürlich, daß die Referenzverteilung bezüglich der verfeinerten Fragmentierung bekannt ist bzw. bestimmt wird (z.B. durch Monitoring der tatsächlichen Referenzverteilung).
Der vorgestellte Allokationsansatz strebt vor allem die Maximierung lokaler Datenzugriffe an, nicht jedoch die Unterstützung von Parallelverarbeitung. Dies wird erst für lokal verteilte Shared-Nothing-Systeme untersucht (Kap. 17), da diese aufgrund der wesentlich effizienteren Kommunikation für die Parallelverarbeitung besser geeignet sind.
[19] Nach Festlegung der partitionierten Allokation könnte in einem zusätzlichen Schritt überprüft werden, für welche Fragmente eine Replikation sinnvoll ist. Unter Leistungsgesichtspunkten wäre dabei eine zusätzliche Allokation an einen Rechner sinnvoll, wenn die damit verbundenen Speicher- und Änderungskosten durch die erwarteten Vorteile für Leser aufgewogen würden.






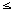 n
n 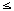 N)
N)





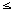 n
n 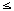 N)
N)